You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
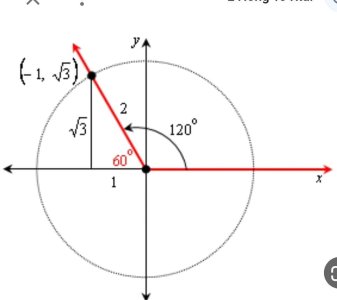
Degree measure in the coordinate plane
- Thread starter Student_0
- Start date
Hi,
Note that this method of assigning angle measures to the circle is not the only common one. Bearing degree measure, often used in navigation and the compass rose, assigns the 0° mark to the positive y-axis and increases angular magnitude clockwise from there.
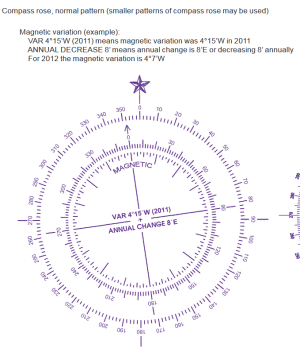
Left is a standard compass rose used by the NOAA and NGA (referenced from the NGA's Section B Positions, Distances, Directions, Compass standard here)
The method of angular measure in your picture occurs primarily in mathematical analysis, which is where it began.
Although this method of positioning the angular measures over a circle did not start in the discipline that became known as trigonometry, a certain practice used in trigonometry (and most mathematics before the invention of mathematical analysis) had a large part in its origin.
In particular, this was the use of primarily nonnegative numbers. Trigonometry and the study of circles before analysis was primarily about measurement of lengths, and lengths were never assigned negative quantities (it would be several hundred years before negative numbers were thought of as real numbers).
While trigonometry began as a set of relations between chords and their intercepted arcs, the invention of the sine measurement (a half-chord associated with half the intercepted arc) made various trigonometric calculations easier than the prior concentration on chord tables.
In many cases, the calculation of sine quantities and related quantities were made easier through the use of right triangles (since bisecting the chord to create a half-chord and half-arc necessarily created a right angle).
The use of sine tables and the complementary leg of the same right triangle, called the complementary sine and eventually cosine, eventually led to a study of triangles all on their own, which became known as trigonometry.
As the sine tables studied the relationship between the angles within a right triangle and the side lengths, not only were all the quantities nonnegative, but all the tables had entries strictly between 0° and 90°, for centuries.
Thus, when the coordinate plane was invented, the sine tables were naturally primarily applicable to right triangles in the so-called first quadrant, where all numbers were nonnegative.
In addition, the first coordinate systems, more properly called ordinate systems, were merely number lines (containing, as usual, only positive numbers) with (only positive) ordinate quantities placed above the line, a bit like a modern bar graph if the bars were line-thin.
Why did our numbers on the number line increase from left to right? Probably because the inventor of the ordinate system, Descartes, wrote and thought in a left-to-right language: French.
This was not the only way: several mathematicians had their number line placed vertically, with ordinates placed left or right of the vertical line. For some reason, the horizontal number line gained greater popularity than the vertical.
While all this was happening, the idea of calculating sine tables via series methods had evolved in several civilizations. Notably, these series methods extended sine values beyond 90° in a continuous, analytic manner.
While this extended sine table (a proto-function) was graphed by many mathematicians in order to reveal the periodicity of the sine values, and their relationship to arcs of the unit circle (they were still concerned primarily with physical measurements), we see Euler, after spending several years studying differential equations and complex numbers, immediately embrace the idea that sine was a function of angle measure (or arclength, he is never quite consistent) in a circle of radius 1 (now often called a unit circle), and immediately, without any hesitation, tell his readers typical values of the sine function, including negative values.
This occurred in his seminal text "Introductio in Analysin Infinitorum", which, due to the incredible results within, and clear exposition, became a sourcebook for mathematicians for the next century and set the standard for the discipline that became known as analysis.
This set the stage for the unit circle as a central figure in analysis, and Descartes and his followers designed the primary method of graphing such figures as numerical relations (Euler laid the groundwork for the first definition of what we now call a function).
From the above, we see how Descartes's left-to-right horizontal number line and the use of, at first, only positive numbers in trigonometry laid the groundwork for placing our 0° angle on the horizontal axis, and traveling upwards (for some reason, most authors placed positive ordinates above their number line instead of below it, when they chose to use a horizontal number line. I cannot speculate on the psychology of this choice, except that most buildings and things of interest to these authors lay above the ground instead of below it).
The placement of the negative number horizontal axis left of the positive number line has a mathematical motive: subtraction was the model for negative numbers at this time, and when we subtract positive numbers on the number line, we move leftwards. Thus, negative numbers, representing positive quantities subtracted from 0, should lie left of 0 in the same way.
Similarly, if one chooses upwards for the positive ordinate axis, it would then make sense to use the same reasoning to locate negative ordinates.
Thus, the coordinate plane was born, and the behavior of the sine function relating positive ordinates with arcs in the first quadrant, starting the counterclockwise behavior you noted above, continues left of the y-axis due to the continuous nature of the sine function, established by its series formula.
Note that this method of assigning angle measures to the circle is not the only common one. Bearing degree measure, often used in navigation and the compass rose, assigns the 0° mark to the positive y-axis and increases angular magnitude clockwise from there.

Left is a standard compass rose used by the NOAA and NGA (referenced from the NGA's Section B Positions, Distances, Directions, Compass standard here)
The method of angular measure in your picture occurs primarily in mathematical analysis, which is where it began.
Although this method of positioning the angular measures over a circle did not start in the discipline that became known as trigonometry, a certain practice used in trigonometry (and most mathematics before the invention of mathematical analysis) had a large part in its origin.
In particular, this was the use of primarily nonnegative numbers. Trigonometry and the study of circles before analysis was primarily about measurement of lengths, and lengths were never assigned negative quantities (it would be several hundred years before negative numbers were thought of as real numbers).
While trigonometry began as a set of relations between chords and their intercepted arcs, the invention of the sine measurement (a half-chord associated with half the intercepted arc) made various trigonometric calculations easier than the prior concentration on chord tables.
In many cases, the calculation of sine quantities and related quantities were made easier through the use of right triangles (since bisecting the chord to create a half-chord and half-arc necessarily created a right angle).
The use of sine tables and the complementary leg of the same right triangle, called the complementary sine and eventually cosine, eventually led to a study of triangles all on their own, which became known as trigonometry.
As the sine tables studied the relationship between the angles within a right triangle and the side lengths, not only were all the quantities nonnegative, but all the tables had entries strictly between 0° and 90°, for centuries.
Thus, when the coordinate plane was invented, the sine tables were naturally primarily applicable to right triangles in the so-called first quadrant, where all numbers were nonnegative.
In addition, the first coordinate systems, more properly called ordinate systems, were merely number lines (containing, as usual, only positive numbers) with (only positive) ordinate quantities placed above the line, a bit like a modern bar graph if the bars were line-thin.
Why did our numbers on the number line increase from left to right? Probably because the inventor of the ordinate system, Descartes, wrote and thought in a left-to-right language: French.
This was not the only way: several mathematicians had their number line placed vertically, with ordinates placed left or right of the vertical line. For some reason, the horizontal number line gained greater popularity than the vertical.
While all this was happening, the idea of calculating sine tables via series methods had evolved in several civilizations. Notably, these series methods extended sine values beyond 90° in a continuous, analytic manner.
While this extended sine table (a proto-function) was graphed by many mathematicians in order to reveal the periodicity of the sine values, and their relationship to arcs of the unit circle (they were still concerned primarily with physical measurements), we see Euler, after spending several years studying differential equations and complex numbers, immediately embrace the idea that sine was a function of angle measure (or arclength, he is never quite consistent) in a circle of radius 1 (now often called a unit circle), and immediately, without any hesitation, tell his readers typical values of the sine function, including negative values.
This occurred in his seminal text "Introductio in Analysin Infinitorum", which, due to the incredible results within, and clear exposition, became a sourcebook for mathematicians for the next century and set the standard for the discipline that became known as analysis.
This set the stage for the unit circle as a central figure in analysis, and Descartes and his followers designed the primary method of graphing such figures as numerical relations (Euler laid the groundwork for the first definition of what we now call a function).
From the above, we see how Descartes's left-to-right horizontal number line and the use of, at first, only positive numbers in trigonometry laid the groundwork for placing our 0° angle on the horizontal axis, and traveling upwards (for some reason, most authors placed positive ordinates above their number line instead of below it, when they chose to use a horizontal number line. I cannot speculate on the psychology of this choice, except that most buildings and things of interest to these authors lay above the ground instead of below it).
The placement of the negative number horizontal axis left of the positive number line has a mathematical motive: subtraction was the model for negative numbers at this time, and when we subtract positive numbers on the number line, we move leftwards. Thus, negative numbers, representing positive quantities subtracted from 0, should lie left of 0 in the same way.
Similarly, if one chooses upwards for the positive ordinate axis, it would then make sense to use the same reasoning to locate negative ordinates.
Thus, the coordinate plane was born, and the behavior of the sine function relating positive ordinates with arcs in the first quadrant, starting the counterclockwise behavior you noted above, continues left of the y-axis due to the continuous nature of the sine function, established by its series formula.